Page 133 -

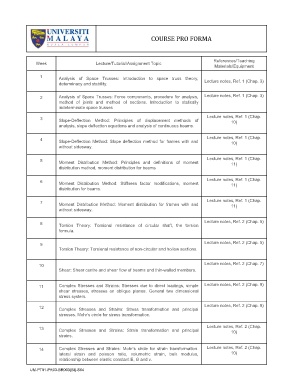
COURSE PRO FORMA

References/Teaching
Week Lecture/Tutorial/Assignment Topic
Materials/Equipment
1 Analysis of Space Trusses: Introduction to space truss theory,
determinacy and stability. Lecture notes, Ref. 1 (Chap. 3)

2 Analysis of Space Trusses: Force components, procedure for analysis, Lecture notes, Ref. 1 (Chap. 3)
method of joints and method of sections. Introduction to statically
indeterminate space trusses

3 Slope-Deflection Method: Principles of displacement methods of Lecture notes, Ref. 1 (Chap.
10)
analysis, slope deflection equations and analysis of continuous beams.

4 Slope-Deflection Method: Slope deflection method for frames with and Lecture notes, Ref. 1 (Chap.
10)
without sidesway.

5 Moment Distribution Method: Principles and definitions of moment Lecture notes, Ref. 1 (Chap.
11)
distribution method, moment distribution for beams

Lecture notes, Ref. 1 (Chap.
6 Moment Distribution Method: Stiffness factor modifications, moment
distribution for beams. 11)

7 Moment Distribution Method: Moment distribution for frames with and Lecture notes, Ref. 1 (Chap.
11)
without sidesway.

8 Torsion Theory: Torsional resistance of circular shaft, the torsion Lecture notes, Ref. 2 (Chap. 5)
formula.

Lecture notes, Ref. 2 (Chap. 5)
9
Torsion Theory: Torsional resistance of non-circular and hollow sections.

10 Lecture notes, Ref. 2 (Chap. 7)
Shear: Shear centre and shear flow of beams and thin-walled members.

11 Complex Stresses and Strains: Stresses due to direct loadings, simple Lecture notes, Ref. 2 (Chap. 9)
shear stresses, stresses on oblique planes. General two dimensional
stress system.

12 Complex Stresses and Strains: Stress transformation and principal Lecture notes, Ref. 2 (Chap. 9)
stresses. Mohr’s circle for stress transformation.

Lecture notes, Ref. 2 (Chap.
13 Complex Stresses and Strains: Strain transformation and principal
strains. 10)

14 Complex Stresses and Strains: Mohr’s circle for strain transformation. Lecture notes, Ref. 2 (Chap.
10)
lateral strain and poisson ratio, volumetric strain, bulk modulus,
relationship between elastic constant E, G and v.
UM-PT01-PK03-BR003(BI)-S04