Page 150 -

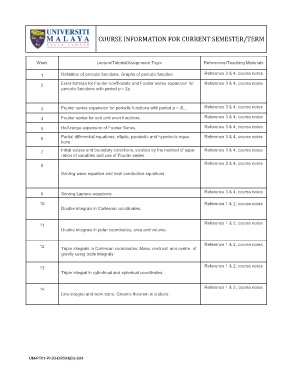
COURSE INFORMATION FOR CURRENT SEMESTER/TERM

Week Lecture/Tutorial/Assignment Topic References/Teaching Materials

1 Definition of periodic functions. Graphs of periodic function Reference 3 & 4, course notes

2 Euler formula for Fourier coefficients and Fourier series expansion for Reference 3 & 4, course notes
periodic functions with period p = 2p

3 Fourier series expansion for periodic functions with period p = 2L, Reference 3 & 4, course notes
4 Fourier series for odd and even functions. Reference 3 & 4, course notes

5 Half-range expansion of Fourier Series. Reference 3 & 4, course notes

6 Partial differential equations: elliptic, parabolic and hyperbolic equa- Reference 3 & 4, course notes
tions.
7 Initial values and boundary conditions, solution by the method of sepa- Reference 3 & 4, course notes
ration of variables and use of Fourier series.
8 Reference 3 & 4, course notes

Solving wave equation and heat conduction equations.

9 Solving Laplace equations. Reference 3 & 4, course notes
10 Reference 1 & 2, course notes
Double integrals in Cartesian coordinates.

11 Reference 1 & 2, course notes
Double integrals in polar coordinates, area and volume.

Reference 1 & 2, course notes
12 Triple integrals in Cartesian coordinates. Mass, centroid and centre of
gravity using triple integrals

13 Reference 1 & 2, course notes
Triple integral in cylindrical and spherical coordinates.

14 Reference 1 & 2, course notes
Line integral and work done. Green’s theorem in a plane

UM-PT01-PK03-BR004(BI)-S04