Page 76 -

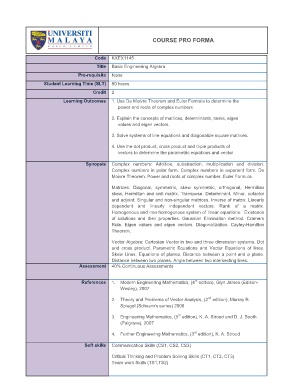
COURSE PRO FORMA

Code KXEX1145

Title Basic Engineering Algebra
Pre-requisite None
Student Learning Time (SLT) 80 hours

Credit 2
Learning Outcomes 1. Use De Moivre Theorem and Euler Formula to determine the
power and roots of complex numbers.

2. Explain the concepts of matrices, determinants, ranks, eigen
values and eigen vectors.
3. Solve systems of line equations and diagonalize square matrices.

4. Use the dot product, cross product and triple products of
vectors to determine the parametric equations and vector

Synopsis Complex numbers: Addition, substraction, multiplication and division.
Complex numbers in polar form. Complex numbers in exponent form. De
Moivre Theorem. Power and roots of complex number. Euler Formula.

Matrices: Diagonal, symmetric, skew symmetric, orthogonal, Hermitian
skew, Hermitian and unit matrix. Transpose. Determinant. Minor, cofactor
and adjoint. Singular and non-singular matrices. Inverse of matrix. Linearly
dependent and linearly independent vectors. Rank of a matrix.
Homogenous and non-homogenous system of linear equations. Existence
of solutions and their properties. Gaussian Elimination method. Cramers
Rule. Eigen values and eigen vectors. Diagonalization. Cayley-Hamilton
Theorem.

Vector Algebra: Cartesian Vector in two and three dimension systems. Dot
and cross product. Parametric Equations and Vector Equations of lines.
Skew Lines. Equations of planes. Distance between a point and a plane.
Distance between two planes. Angle between two intersecting lines.
Assessment 40% Continuous Assessments

th
References 1. Modern Engineering Mathematics, (4 edition), Glyn James (Edison-
Wesley), 2007
nd
2. Theory and Problems of Vector Analysis, (2 edition), Murray R.
Spiegel (Schaum's series) 2008

th
3. Engineering Mathematics, (5 edition), K. A. Stroud and D. J. Booth
(Palgrave), 2007
rd
4. Further Engineering Mathematics, (3 edition), K. A. Stroud
Soft skills Communication Skills (CS1, CS2, CS3)

Critical Thinking and Problem Solving Skills (CT1, CT2, CT3)
Team work Skills (TS1,TS2)